A guest blog by Richard Raddick

Introduction

The word “survivor” designates the beneficiary of an improbable outcome, not infrequently the result of pure chance. In this sense, every no-motto half eagle in existence today is a survivor. As we shall see, experts estimate that there are perhaps 45,000 of these coins, the remnant of an original mintage of over 11,000,000. In other words, the odds against survival for these coins were on the order of 250-to-1, which qualifies as improbable. Among these survivors, I believe that somewhat more than 3,600, or about 8%, are Fairmont coins.

Indeed, when the dust finally settles, I think it is likely that the Fairmont hoard will be recognized as the largest single source for these coins. As such, it seems natural to ask whether the date/mint distributions of the Fairmont No Motto half eagles can tell us anything interesting about the corresponding distributions of the entire population of surviving no-motto half eagles. Conversely, discrepancies may reveal facts about the makeup the Fairmont hoard, itself, which are not otherwise obvious.

This is a change in emphasis. In the prior articles of this series, I have been mainly concerned with determining the number of Fairmont coins. Now, I will be using that information to investigate whether those numbers tell us anything useful or interesting about the overall population of surviving US gold coins, starting with those I know best, the no-motto half eagles.

In the next section, I will discuss survival estimates and their limitations. Following that, I will present a comparison between these estimates and the Fairmont numbers in graphical format. Finally, I will discuss the results.

Survival Estimates

In principle, the most straight-forward way to determine the number of surviving no-motto half eagles would be to count them. In practice, this does not work very well because, unlike bank notes, coins do not carry serial numbers.

Of course, third party grading (TPG) slabs do, but the problem here is unrecognized re-submissions and selection bias that distort the counts. Rusty Goe, for example, is firmly dismissive of TPG data serving as survival estimates:

The concept of population data derived from PCGS and NGC population (or census) reports serving as actual totals of extant coins is a worn-out paradigm that does not accurately reflect true supplies. The phrase, “PCGS has graded such and such a number of a specific date-denomination,” simply based on the submission events total recorded in PCGS’s database, is misleading and needs to be relegated to the trash bin of numismatic jargon.

A sense of the difficulties with TPG data may be conveyed by noting that, as of late December, 2024, PCGS reports that it has graded 27,442 No Motto half eagles (Classic Heads and No Motto Liberty Heads, combined), and NGC reports grading 28,595, with another 10,000 (yes–that’s the precise number!) receiving NGC-Details grades. PCGS does not report its details grades, but assuming a number comparable to NGC, the implied total is about 76,000 NM half eagles, about 1.7x the number of survivors estimated by the experts.

In this respect, the Fairmont coins are unusual because PCGS data, either through direct inspection or from time-series analysis, do more-or-less “accurately reflect true supplies.” We may never again be so lucky.

Selection bias is also at work. Briefly, it is more likely that a run-of-the-mill no-motto half eagle from one of the branch mints (Dahlonega, say) will be submitted to NGC or PCGS for grading than a similar, common-date coin from Philadelphia.

OK–direct enumeration does not work, and using TPG census numbers as a proxy does not, either. What about other proxies?

Some 45 years ago, David Akers used sales records to estimate relative rarity. At the time, this was a creative approach, but in hindsight, it suffered from the same problems as estimates based on TPG data - multiple counts and selection bias. To his credit, Akers recognized the first of these, but it is less clear that he considered the second, which stems from the practice of sales being organized as date runs, often with a single example per variety, which thereby caps the numbers for the common dates. Thus, Akers tended to underestimate systematically the relative number of survivors for the common varieties.

What about mintage numbers?

**1852-C $5.00 PCGS AU55+ CAC, Fairmont**

In a previous article in this series, I showed that mintage numbers, segregated according to mint and adjusted for loss through attrition, work surprisingly well to model the number distribution of the Fairmont NM $5s, but this is likely, once again, to be a one-off. The Fairmont NM $5s are almost certainly a relatively well-mixed sample of the overall population of no-motto half eagles that is, itself, likely to be unusually well-behaved, in the sense that its individual issues evidently shared, in common, more-or-less the same loss history.

In other words, among the No Motto $5s, the survival numbers for the various individual issues do not appear to be strongly affected by idiosyncratic events–a ship wreck, the arbitrage activities of speculators, or government actions–rather, to the extent that events affected the population (and they certainly did), they appear to have affected all the issues more-or-less equally. Thus, although perhaps only 0.4% of the original total issue of no-motto half eagles survive today, this number is probably roughly descriptive for all the varieties within the series. This circumstance may also apply to the no-motto eagles and double eagles (the 1857-S $20s are a well-known exception), but certainly not to the overall population of US gold coins.

All of which leads us to expert knowledge: experts such as Doug Winter or Rusty Goe tell us how many survivors they believe exist within their areas of specialization. I suspect if someone were to ask Doug or Rusty: “How do you know”? the answer would be along the lines of “From decades of observation and study as a dealer and a specialist, with both a keen interest and an economic stake in getting it right.”

In our “information age” of digital computers, expert knowledge presents a bit of a problem, because it tends to be difficult to quantify or convert into an algorithm. The current effort to do so is part of artificial intelligence, or “AI” - in my day, we called it machine learning. Same thing, different packaging.

In this article, I will use two sources of expert knowledge for survival estimates for the No Motto half eagles: Doug Winter’s numbers and the Survival Estimates in the PCGS CoinFacts database. According to PCGS:

… the survival estimates … represent the consensus opinion of the PCGS CoinFacts Board of Experts. PCGS CoinFacts maintains an internal data base of survival estimates for all United States coins. Members of the PCGS CoinFacts Board of Experts (which include many of the top rare coin experts of all-time) list their estimates of survival rates in this data base. The figures … represent the average of the experts’ opinions.

Sounds impressive, perhaps, but beyond this, PCGS does not tell us much. We do not know who the “Board of Experts” are, or how many opinions are included in each consensus estimate (presumably the number varies, but it is probably rarely a very large number), what the range of the estimates is, or how often they are updated. To me, it looks like updates are rather infrequent, which raises the possibility that the estimates may be out-of-date. What I do know is that there have been no changes whatsoever among the PCGS survival estimates for the No Motto half eagles between late 2020, when I first transcribed the numbers, and late 2024, when I reviewed them. The PCGS survival estimates for half eagles almost certainly do not reflect the Fairmont coins - we first learned of the existence of Fairmont half eagles in August, 2020.

**1853-D Large D $5.00 PCGS AU53, Fairmont**

About Doug’s estimates, I know quite a bit more. Obviously, I know who made them, and also when they were made: for Charlotte, 2008; for Dahlonega, 2013 and again in 2023, for New Orleans, 2006 and again in 2018, and for Philadelphia and San Francisco, 2024. Doug kindly provided me with his Philadelphia and San Francisco estimates privately; for the others, I extracted the numbers from his books. Instead of a single number, Doug typically cites a range, and he sometimes hedges the upper bound a bit by using notations like “+” and “++” - presumably he means “perhaps more” and “perhaps considerably more” by these. Whether Doug’s estimates reflect the Fairmont NM $5s is unclear: obviously, his numbers for Charlotte cannot, but some of his more recent estimates may.

Of course, experts can disagree, sometimes dramatically. Perhaps the textbook case among the NM $5s is the 1854-S issue: both the PCGS Board of Experts and Doug believe there are three known examples, but the experts at NGC claim there are four. The difference lies in how two questions are answered: (1) Does the coin that was stolen in 1967, and never recovered, still exist? and (2) Is the 2018 discovery genuine? The NGC experts evidently believe that the answer to both questions is “Yes,” whereas the PCGS experts and Doug believe that the answer to one of the two questions is “No.”

The table below presents the composite numbers. The lack of consensus is striking, especially for the Philadelphia No Motto Liberty $5s and the Charlotte half eagles. In both cases, I think Doug is probably right, and I base this opinion in no small part on what I know from studying the Fairmont coins.

Among the Fairmont NM $5s, there simply are not almost twice as many coins from Charlotte as from Dahlonega - in fact, the numbers are almost exactly the same. Nor are there almost as many half eagles from Charlotte as there are NM $5s from Philadelphia, as the PCGS survival estimates suggest - in fact, there are 10x as many from Philadelphia. Even allowing for incomplete mixing among the Fairmont coins, it is hard to reconcile the numbers, and I, quite frankly, believe mine.

Doug estimates that there are considerably more NM half eagle survivors from Philadelphia than the PCGS numbers suggest, and that there are many fewer Charlotte half eagles than the PCGS estimates imply.

If we simply adopt the midrange from Doug’s estimates, there are some 35,000 surviving NM $5s, excluding the Classic Head issues from Philadelphia. The PCGS estimates suggest there are about 5,000 Classic Head $5s. Doubling that number to more-or-less match what Doug’s estimate might have been, had he made one, I arrive at perhaps 45,000 extant NM half eagles, the number I cited in the introduction.

Analysis

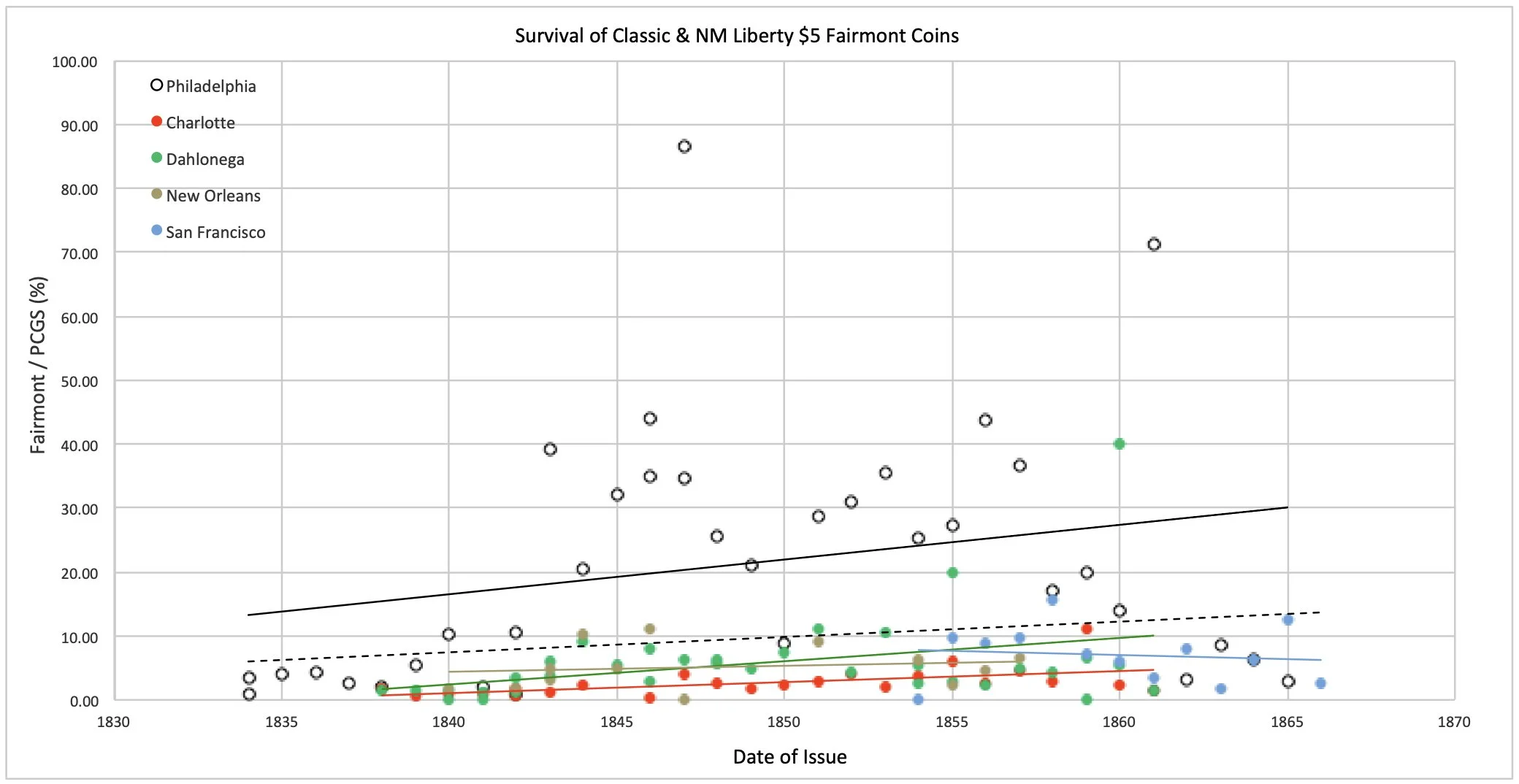
The figure below shows, for each No Motto half eagle variety, the ratio of the number of known Fairmont coins and a survival estimate derived from Doug’s numbers, expressed as a percent. For the survival estimate, I simply adopted the average of the lower and upper limits that Doug cites. For example, I believe there are eleven 1839-P half eagles among the Fairmont coins. Doug’s survival estimate for this issue is 300-400+ coins, so the value plotted is 11 / (300+400)/2 x 100% = 3.14%. For several of the Dahlonega intra-date varieties, I apportioned Doug’s estimate according to what he wrote in the text of his book.

The series for each of the five mints is plotted separately, and superimposed on the data points for each mint is a trend line, which is the linear least-squares best fit to the data. The trend line for all issues from the five mints, combined, is also shown as the dashed line.

If everything were perfect: if Doug’s survival estimates were spot-on, and the Fairmont coins were a truly representative, fully-mixed sample of the overall population, all the trend lines would be flat, they would all coincide, and the data points would lie on them. There would be little more to say.

In fact, none of this is true. The Philadelphia trend line clearly lies above those for the four branch mints, and the San Francisco trend line lies a bit below the others. None of the trendlines are flat (although the Philadelphia line is nearly so), but rather, they all slope upward toward the right, the Charlotte & San Francisco lines more steeply than the others. And, of course, the individual data points are scattered, which is presumably the random variation, which is to be expected.

When I use the PCGS survival estimates, rather than Doug’s numbers, these patterns become accentuated, as shown in the figure below. The separation of the Philadelphia trend line from the others becomes more extreme, and it also develops a pronounced upward slope, which turns out to be almost entirely due to the six Classic Head issues that are now included in the Philadelphia data (Doug did not provide survival estimates for these six issues). The Charlotte trend line drops below those for the other two Southern mints, and the San Francisco trend line now slopes downward from left to right.

What is wrong: is it the Fairmont data, the survival estimates, or both? In the remainder of this article, I will explore this question, dividing the discussion into two parts: (1) the relative locations of the trend lines, and (2) the slopes of the trend lines.

Discussion

The relative positions of the trend lines could reflect an excess of Philadelphia NM half eagles in the Fairmont hoard (and, less clearly, a deficiency of San Francisco coins), relative to expectation, or it could point to a tendency among the experts to under-estimate the number of surviving Philadelphia No Motto $5s. In fact, I suspect it may be some of each.

I have already indicated that I believe the PCGS CoinFacts Board of Experts, as a group, grossly underestimate the number of surviving NM half eagles from Philadelphia. This tendency may go back a long time. For example, I think that David Akers’ use of sales records to estimate relative rarity led him to underestimate systematically the number of survivors for the common varieties of gold coins. Among the No Motto half eagles, the common varieties are Philadelphia issues (the 1844-O being a notable exception to this rule).

This bias may be rooted in our coin collecting and sales practices: we tend to emphasize date sets. To offer a specific example, there may100x more surviving 1861 half eagles than 1865 $5s, but that does not mean that most collectors own 100 1861 coins to complement their single 1865, nor that most auctions offer 100 1861 half eagles whenever they feature an 1865 example. More likely, there will be a single 1861 (or, at most, a few), but much nicer coins.

In general, we tend to depreciate the commonplace. Everyone knows there are many more 1861 half eagles than 1865 coins, but a stubborn desire to precisely quantify this excess is, perhaps, viewed as a bit obsessive. I plead guilty.

I strongly suspect, however, that there is more to it than just this, and, in order to argue the point, I will begin with a detour into the process that, in physics, is called diffusion.

Consider a thought experiment. Suppose you have a bowl of still water, and you gently drop into it, perhaps near the edge, a single drop of water-soluble food coloring, perhaps red, and then watch what happens, without further disturbing the liquid. What you will observe is that the colored drop expands and becomes less intense in color. If you wait long enough, perhaps hours or even days, the drop eventually loses its identity, and the entire bowl of water becomes the same color of pink. This process is called diffusion, and the end result is a fully-mixed bowl of dye and water. I have already used the term “mixed” on several occasions in this article, and this is what I mean by it.

Now consider a slightly more complicated experiment. Suppose you drop red dye into the bowl on one side, and blue dye on the other, and then focus your attention on what happens at a specific location that is close to, but not at, the red drop. At first, the water at your observing location is red, albeit less intensely with time, but eventually, blue color also starts to obtrude, increasingly, with time. The mixture at your location starts to turn a bit purple, and becomes increasingly so until full mixing eventually happens. This thought experiment illustrates that diffusion progresses in two directions - away from a source, and into locations distant from a source.

I find the concept of diffusion useful as I think about the circulation of coins, and the makeup of the coins in the Fairmont hoard. A hoard is a sample of the coins available at the time and place of its formation. In the case of the Fairmont hoard, we know formation was not before 1932 - there are 1932 eagles in it. Of course, it may have been formed over an interval of several years, as a growing accumulation, but the process ended no earlier than 1932.

I have also long suspected that the place of formation was in the Northeast (likely New York City), or possibly the Midwest (e.g., Chicago), or perhaps even Canada, (e.g., Toronto), but quite clearly it was not in San Francisco or New Orleans.

So, imagine a diffusion experiment, with five sources (Philadelphia, the three Southern mints, and San Francisco), and we run the experiment in New York City for 67 years (for the 1865 coins) up to 98 years (for the 1834 coins). What would we observe in 1932? Unless the process has run to its fully-mixed state, which I believe is unlikely, we would observe a relative surplus of Philadelphia coins, a deficit of Southern coins, and an even more pronounced deficit of San Francisco coins. And, this is what we do, in fact, observe!

In the previous article in this series, I described how the Philadelphia No Motto $5s appear to be over-represented in the Fairmont hoard, relative to the Southern coins, and the San Francisco coins are under-represented, also relative to the Southern coins. It is important to emphasize that this pattern is independent of differences in mintage - the analysis in that article specifically removed all such dependence. And now, we apparently see the same pattern again, when we control for differences in the expected number of survivors, rather than mintage. So, the pattern is not due to mintage, and it also seems unlikely to be due wholly to bias in the survival estimates, although a degree of such bias may exist. Rather, I suspect that the explanation is incomplete diffusion. I think that the Fairmont numbers are telling us is that the process had not yet had time to run to the end-state of full mixing at the place where the Fairmont hoard was formed, a location that was considerably closer to Philadelphia than the Southern mints, let alone San Francisco. New York City seems a plausible candidate.

The defining characteristics of the Fairmont hoard are its size and breadth, along with the fact that it seems to be fairly well mixed, although not fully. Most of its older coins, including its No Motto half eagles, are lightly circulated, but not heavily worn - evidently, they spent some time in circulation, but not too much. Considerable mixing undoubtedly occurred during this circulation.

For No Motto gold coins, including the half eagles, the pivotal event was the outbreak of the Civil War, which led to the wholesale withdrawal of gold coinage from circulation, and its replacement with paper currency. What happened after the War, however, is less clear. Some of the sequestered coins presumably returned to circulation, but others joined the ever-growing accumulations of US gold coins in bank vaults. Some were probably exported, although this did not become a widespread practice until the late 1870s. In any case, much of the post-War diffusion probably occurred in the form of coin movements between banks, rather than commercial circulation. Whatever their history, however, I think it is likely that the Fairmont No Motto half eagles spent most of their existence resting quietly in vaults.

There is a lot to think about here, and I have only begun the process. There are other ways to analyze the data besides separating it by mints - separation by rarity, for example - and such analyses may offer additional insight. Of course, there are also the half eagles from Carson City, which have not yet entered into the analysis, as well as the eagles and double eagles.

As preliminary conclusions, however, I believe that Doug’s survival estimates for the Philadelphia NM $5s may eventually prove to be more-or-less correct. I also think that the PCGS survival estimates for Philadelphia NM $5s are systematically and significantly low, and their estimates for Charlotte half eagles are much too high.

The slopes of the trend lines present a more vexing problem, if only because I simply cannot think of a persuasive explanation, regardless of whether the source lies with the survival estimates or the makeup of the Fairmont hoard.

To blame it on the experts would be to argue that, for some reason, their methodology contains a systematic, pervasive bias that leads them to overestimate the number of survivors for the older issues, and underestimate the number for the newer issues. Furthermore, this bias must be operative within the realm of the NM $5s, between 1834 and 1866. It is not, for example, 19th century vs 20th century, or even 1850s vs 1880s. So, far, I have not come up with anything that I find convincing.

If it is difficult to find a reason to blame the problem on the experts, it is no easier to imagine how it could be something about the makeup of the Fairmont hoard, at least as I now understand it. What it would require is something about the hoard that leads to unexpectedly high numbers of the newer issues within the series of No Motto half eagles, relative to the older coins.

It cannot be attrition from circulation wear. Attrition is implicitly accounted for in the survival estimates from the experts. The whole point of survival analysis is to assess, issue by issue, how many coins managed to avoid all the loss mechanisms that the coins faced. For this purpose, attrition is just another one of these loss mechanisms. Accordingly, when I normalize the Fairmont numbers by the survival estimates, I normalize away any possible dependence on attrition, just as, in the previous paper, I normalized away any possible dependence on mintage when I created the PPM parameter.

It also seems unlikely to be an effect of diffusion. The difficulty is that the trend lines for all five mints slope upward, left to right, whereas diffusion would predict that one of them (for the mint closest to the hoard’s home location) would slope upward (i.e., more newer coins), but the others would probably slope downward (i.e., more older coins).

In fact, the only mechanism I have been able to imagine that might explain this behavior is if the Fairmont coins are undercounted in a very specific way: they become increasingly undercounted as the age of the coins becomes greater. This could happen if a significant number of heavily worn or damaged coins in the hoard were never graded. Presumably, these would tend to be the older coins, so the result would be an over-representation of the newer coins in among the counted Fairmont No Motto $5s. In particular, this could explain the apparent shortage of Classic Head coins among the Fairmonts.

The problem with this explanation is the scarce and rare coins. In the context of this discussion, I think it is reasonable to argue that few, if any, of the half eagles from Charlotte or Dahlonega would have been left ungraded - they are all scarce, relative to, say, the common-date Philadelphia issues. Yet the trend lines for the coins from these two mints show the positive slope as Philadelphia - indeed, the Charlotte trend line has the steepest slope - implying that scarcer issues - e.g., from Charlotte & Dahlonega - share in whatever purported anomaly within the Fairmonts may be creating the troublesome behavior.

**1862-S $5.00 PCGS AU53 CAC, Fairmont**

Furthermore, if anything, the Fairmont coins seem to be characterized by too few examples of rarities, rather than too many, and this tendency would be exacerbated by culling. For example, it seems noticeably peculiar that there have been no 1847-O half eagles among the Fairmont coins, given the known size of the hoard. If truly substantial numbers of Fairmont coins were withheld from grading, this problem would become worse, and eventually we would have to wonder, not only why there were no 1847-O half eagles, but also no 1854-S half eagles, among the Fairmont coins. I think we can rest assured, if there had been an 1854-S half eagle in the hoard, we would know about it, regardless of its condition! And likewise with all the other rarities - none of those coins would have been culled.

Accordingly, I tend to discount stories that large numbers of heavily worn and/or damaged Fairmont coins have been culled and (perhaps) melted. As I argued in the third article in this series, there is evidence that some Fairmont coins, indeed, were never graded. There is, however, also evidence (e.g., from the success of the attrition model) that the numbers of No Motto half eagles that were culled is probably not too large, except perhaps for a few of the most common issues - 1861, in particular.

All of which leads me to conclude that something is going on here that I do not yet understand. The “Aha!” moment, if there is to be one, has not yet happened. Luckily, there is an abundance of possibilities for further study, and these may eventually help resolve some of the present difficulties.

The following appendix contains summary data for all 121 issues of No Motto half eagles, organized by mint.

For each issue, I have tabulated the survival estimates from both PCGS and Doug Winter, and the number of Fairmont coins I believe to exist. The trend lines permit the calculation of how many Fairmont coins *should* exist, if we assume that Doug’s survival estimates are precisely correct, or, conversely, how many survivors should exist, if we assume that the Fairmont coins are truly representative of the overall surviving population on a mint-by-mint basis - in other words, I am allowing for the possibility of incomplete mixing between mints, but I assume full mixing for the coins from each mint. These numbers are presented in the columns headed “Model Pred.” - they provide a sense of how much still needs to be explained. Of course, some of the discrepancies are simply statistical scatter, which is to be expected.

The Roman Senator Cato the Elder supposedly concluded all his speeches, on whatever subject, with the same words. In the spirit of Cato, I will conclude this article with an abbreviated version of my customary ending: I wish we had the actual inventory numbers for the Fairmont hoard.

Blog

Fairmont Gold Pieces, Part VIII: The No Motto Half Eagles - Survival Estimates

Douglas Winter Numismatics

Search our Blog/Articles